[Note on manuscript references: This is taken directly from Chapter 6 of my 1988 dissertation. The bold-faced JC and DT designations refer to specific manuscripts which, at that time, were not part of any library collection and had not been cataloged or given any kind of identifiers. The JC items were in John Cage’s possession and the DT items belonged to David Tudor. I gave them numbers of my own devising and included a catalog as an appendix to the dissertation.]
[Note on figures: Clicking on the figures will display them at full size.]
Copyright 1988 by James Pritchett. All rights reserved.
After completing Williams Mix, assisting Earle Brown with the preparation of his Octet for magnetic tape, and organizing the electronic music concert at the University of Illinois, Cage returned to New York to start on a new project. Cage’s vision was grand:
From time to time ideas come for my next work which as I see it will be a large work which will always be in progress and will never be finished; at the same time any part of it will be able to be performed once I have begun. It will include tape and any other time actions, not excluding violins and whatever else I put my attention to. I will of course write other music than this, but only if required by some outside situation.[1]
Cage’s plan was to compose many independent pieces for various media, each of which could be played as a self-contained work in its own right, or could be performed together with any number of the others. Such an open work could be added to constantly — since the ensemble would not be fixed at any time, the total need never be “finished”, but would remain a work “in progress.”
This large-scale project occupied Cage at various times during the period of 1953 until 1956, at which point he dropped the plan altogether and moved on to other concerns. In the course of these three years, however, Cage produced a number of pieces which represent partial realizations of his original plan. These are: six short pieces for a string player (1953), an unfinished work for magnetic tape (1953?), an unfinished work for voice (1953?), 34′ 46.776” for a pianist (1954), 31′ 57.9864” for a pianist (1954), 26′ 1.1499” for a string player (1955), and 27′ 10.554” for a percussionist (1956).
The individual parts of Cage’s open-ensemble work were to be unified through their use of a common rhythmic structure. This rhythmic structure, however, was to be different in its conception from those of Cage’s previous works, in that it would be open rather than closed. We have already seen (in Chapter 5) Cage’s use of a simple open structure for the Music for piano 4-19. This set, conceived at the same time as the open-ensemble project, consisted of 16 independent, equal-sized units — the individual one-page pieces. Any number of these units could be performed in any horizontal or vertical combinations. The individual pieces, in other words, were structural “blocks” that could be used to construct a myriad of different forms.
In his new project, Cage was to apply this principle to rhythmic structure. Rather than treat rhythmic structure as a whole which was divided into parts, Cage decided to think of it as a series of units: the phrase groups of his structure. As will be recalled, the phrase group units of a rhythmic structure were all of the same length, so that this conception of rhythmic structure would parallel the overall structure of the Music for piano 4-19: the new work would become a series of independent, equal-sized units. The various parts of the new ensemble piece would all have the same overall rhythmic structure (in other words, the same number of phrase groups), but any number of these units could be performed in any horizontal or vertical combinations. The permutability of the structure at the level of the phrase group would allow a piece as short as a single phrase group to be a complete, performable part of the ensemble work.
The structure Cage arrived at for the ensemble piece was on a grand scale itself: 13 parts with the proportions {3, 7, 2, 5, 11, 14, 7, 6, 1, 15, 11, 3, 15}. This structure is listed in documents JC/19 (for the short string pieces) and JC/131 (for the unfinished tape piece). The sum of the proportions is 100, so that the overall structure would consist of 100 units (phrase groups) of 100 measures each, or a total of 10,000 measures. In his lecture “45′ for a Speaker”, Cage confirms this structure: “It just happened that the series of numbers which are at the basis of this work add up to 100 x 100 which is 10,000.”[2] That Cage says this structure “just happened” suggests that the structure was randomly derived, perhaps in a way similar to the structure of Williams Mix.[3] In any event, the number 10,000 had a significance for Cage: “That [the structure is based on 10,000] is pleasing, momentarily: The world, the 10,000 things.”[4] Cage refers here to the symbolism of the number 10,000 in oriental philosophy and writing, where it represents the infinite. “The Ten Thousand Things” is a common phrase found in Taoist and Buddhist writings to connote the material diversity of the universe. Lao Tzu, for example, writes in the Tao Te Ching:
Tao produced the One.
The One produced the two.
The two produced the three.
And the three produced the ten thousand things.[5]
Cage refers to this not only in “45′ for a Speaker”, but also in his notes for parts of the ensemble piece. Under the list of structural proportions in JC/19 is the comment: “100 x 100 (The 10,000 Things)”, and DT/16, which may be a title page for the unfinished tape piece, bears the inscription “The Ten Thousand”. While the individual pieces were each given titles based on their durations, Cage never publicly gave a title to the ensemble project as a whole. In this chapter, I will take advantage of the “accidental” poetry of the structure, and refer to the general plan for the work as “The Ten Thousand Things”.
The proposed structure of 10,000 measures was too large to be manageable. Music of changes, Cage’s largest chance-composed work thus far, was only about 877 measures long, and had taken nine months to complete. Even a single phrase group, the smallest independent unit of the piece, would be 100 measures in length. Therefore, Cage decided to reduce the size of the structure by reducing the size of a single unit. He changed the structure, making the phrase group units 100beats in length, rather than 100 measures, so that the overall structure would be 100 units of 100 beats each, or 2500 bars of 4/4 meter.
This smaller unit size required a change in the phrase structure of a unit. According to the principles of rhythmic structure, the phrase group should consist of 13 phrases following the proportion series. Since Cage was now measuring his phrase groups in beats rather than in bars, this would result in phrases that were too short to be useful — phrases would be as short as a single beat. Cage’s solution, documented in JC/19 and JC/131, was to form larger groupings of the 13 structural proportions as follows: {3,7,2; 5,11; 14,7,6,1; 15,11; 3,15}. This resulted in five phrases with lengths of 12, 16, 28, 26, and 18 beats, respectively, or, 3, 4, 7, 6.5, and 4.5 measures of 4/4.
To summarize the planned structure of each individual piece of “The Ten Thousand Things”: each unit of the piece would consist of five phrases with proportions {3, 4, 7, 6.5, 4.5}, for a total of 25 bars of 4/4, or 100 beats. These units would in turn be grouped to form 13 sections, with proportions {3, 7, 2, 5, 11, 14, 7, 6, 1, 15, 11, 3, 15}, for a total of 100 units, or 2500 bars of 4/4, or 10,000 beats. In short, there were two separate proportion series in this work: a 5-part structure which functioned only at the small scale, and a 13-part structure functioning only at the large scale. This structure was the basis for all of the pieces produced during this time, although variations were to occur from piece to piece. In fact, the large-scale plan — works of 100 units each — was never fully realized, with the four largest works each consisting of only 28 units.
Six Short Pieces for a String Player (1953)
The first works to be composed in this large “never-ending” project were six short pieces for a string player. Composed between May and July of 1953, each of these pieces is only one phrase group long, confirming Cage’s plan to have the phrase group as the basic self-contained unit of the overall work. The titles of the pieces were simply their durations, roughly calculated in minutes and seconds. Figure 6-1 is a listing of the titles, along with the dates of completion as found in the scores. The first five of these pieces were ultimately to become part of the larger string piece 26′ 1.1499” for a string player, while the last piece, 59 1/2” for a String Player, remained independent.

The notation of the pieces is a graphic one, as illustrated by the sample in Figure 6-2. In the notation, time is measured in a manner similar to that of Music of changes, in that 2 centimeters here equal one beat. The tempo changes with every phrase: therefore, at the beginning of each phrase, Cage put a 2 centimeter “ruler” with the new tempo marking.
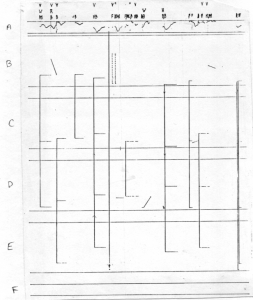
Vertically, the four large areas or bands (marked B through E in the figure) represent the four strings of the instrument being played, from highest to lowest. The vertical placement of points within these bands indicates the location at which the strings are to be stopped, so that the vertical dimension within each band corresponds to pitch, although the four bands as a whole do not represent a continuous pitch field. Points connected by vertical lines represent multiple stops, with the arrows giving the direction of breaking triple or quadruple stops. In those places where such arrows are not drawn, the direction of breaking is left to the performer’s choice. This notation allowed the pieces to be performed on any four-stringed bowed instrument (violin, viola, cello, or contrabass), although in Cage’s notes for the pieces (JC/20, JC/22, and JC/24) he refers to these as “violin” pieces.
The smaller band below the four string bands (marked F in the figure) represents “noises on the box [of the instrument], sounds other than those produced on the strings.”[6] The vertical placement of points and lines within this band gives the relative pitch of the noise, which “may issue from entirely other sources, e.g. percussion instruments, whistles, radios, etc.”[7]
The smaller band above the string bands (marked A in the figure) represents the bowing pressure, or amplitude of the sounds. This is notated graphically so that the top of the band is the least pressure (softest) and the bottom the most pressure (loudest). The notations here correspond one-to-one with the sound notations below them. In the case of sounds that extend in time, a pressure “curve” is notated, showing the changing amplitude of the sound.
The notations at the top of the page also relate to bowing. The traditional up and down bow symbols are used. The letters H and W (“Hair” and “Wood”) denote ordinario and col legnobowing. The letters F, N, and B give the location of the bowing: F stands for fingerboard (sul tasto), N stands for normal, and B stands for bridge (sul ponticello). Compound notations denote intermediate positions. FN and NF are both between fingerboard and normal: FN is closer to the fingerboard, while NF is closer to normal. Similarly, NB and BN are locations between normal and the bridge.
The method of composition Cage devised for the string pieces (and which he was to use for all the pieces of “The Ten Thousand Things”) was a variant of the paper imperfection method used inMusic for piano. In those works, each point had represented a single, complete sound event. These simple point events, it will be recalled, specified pitch and attack time, but not duration. As noted in Chapter 5, Cage found this method to be too simplistic, and in the new work he set out to improve the method so as to produce more varied results.

These new ideas are sketched out in JC/20, a page of notes Cage made early on in the composition of the short string pieces (see Figure 6-3, top half). Cage realized that the points could generate more complex events by extension into the space of the page. If extended horizontally (“back or forth”), a line event, or one “maintaining pitch” could be created. Through vertical extension (“up or down”), an aggregate or chord could be obtained. Finally, the point could be extended along any arbitrary curve or angle in the pitch-time space of the notation to produce a slide of any contour. These events, possessing duration, could thus be either whole or fragmented in time (“constant or intermittent”).
Cage’s strategy in composing each individual sound event in all the pieces of “The Ten Thousand Things” was essentially the same. First, he would define the general structure and duration (measured in terms of points) of each event of the piece. Then he would use the vertical and horizontal placement of the randomly-inscribed points to provide specific pitch and rhythm for these abstract event structures. In other words, the structures or shapes of the events were limited in number and selected by Cage. The particular pitch and rhythmic content of the individual manifestations of each event type would be wholly random, selected by the point-drawing technique from the continuum of possibilities.
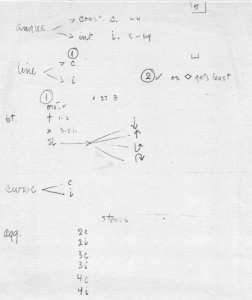
The means of determining the structures of each event was through consultation of the I Ching. Given a number N categories of event types, Cage would divide the 64 possible hexagrams of the I Ching into N parts. This was done by tossing N-1 hexagrams and using these as the dividing points for the partition. Cage derived this method in his notes on JC/20 (see Figure 6-3, bottom half). Here, Cage planned on using four categories of sound events: “maintaining” (lines), aggregates, angles, and curves. To divide the I Ching into four parts, he tossed three hexagrams: they happened to be 58, 19, and 24. These served as the points of division for the four I Ching bands, so that a hexagram number between 1 and 19 would denote a line event, 20 to 24 an aggregate, 25 to 58 an angle, and 59 to 64 a curve.[8]
This method of randomly determining the division of the I Ching served two purposes. First, it allowed Cage to use the I Ching to select easily from any number of possibilities (up to 64). In earlier works using the I Ching, Cage had tried to limit his selection to even divisions of 64 (such as the 8 superimposed parts of Music of changes). This new method freed Cage from any such restrictions, providing him with as easy a means of dividing the I Ching into 17 parts as 8, or any other number. Secondly, it created a random distribution of probabilities for each event type. Rather than have a homogeneous blend of equal amounts of all possibilities, the random division method insured that the mix of events would be dynamic over the course of the piece.
The first stage in the process of composing each of the six short string pieces was to determine the tempi for each of the five phrases. According to JC/19, these were in the range of 40 to 208 beats per minute Although no chart of tempi exists, it can be assumed that one did exist, probably similar in structure to the tempo charts of Music of changes and similar pieces, with 32 tempi and 32 blank cells (the blanks representing maintenance of previous tempo).
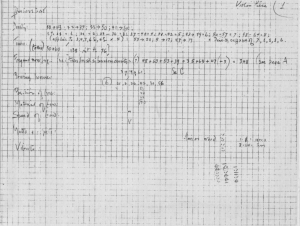
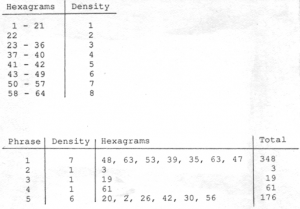
The next step was to calculate the number of points to be inscribed in each phrase. This was a two-step process: first a density value from 1 to 8 was selected (using a random partitioning of theI Ching), and then that many hexagrams were obtained and added together to produce the number of points. Document JC/22 (Figure 6-4a) is a worksheet for the first string piece (57 1/2” for a String Player), and it shows the means by which the number of points for each phrase was determined (summarized in Figure 6-4b). First, Cage divided the I Ching into eight parts by tossing seven hexagrams: 43, 22, 37, 23, 50, and 47. This resulted in the density table shown at the top of Figure 6-4b. Five more hexagrams were then tossed to select densities for each of the five phrases, using this table of hexagrams. The five hexagrams tossed (53, 20, 5, 17, and 47) corresponded to densities of 7, 1, 1, 1, and 6. More hexagrams were tossed to be added together, as shown at the bottom of Figure 6-4b. Therefore, the five phrases of this piece contained 348, 3, 19, 61, and 176 points, respectively. Document JC/24 lists the number of points in each phrase of the first four short string pieces.
At this point, Cage determined the sequences of sounds and silences for each phrase, their durations, and, in the case of sounds, the general type of event. There were seven types of sound events: points (i.e., pizzicati), lines (sustained tones), aggregates (multiple stops), angles (linear slides), curves (non-linear slides), noise points (noises of no duration), and noise lines (noises of some duration). A randomly distributed I Ching table was established for these seven types at the start of each phrase (using the method outlined above).
Each sound or silence was derived from a single hexagram number. Even numbers represented silences, while odd numbers represented sounds. The type of sound event was determined by the distribution table for that phrase. This same hexagram number determined the duration of the sound or silence, measured in points. For silences, hexagram numbers of 2 through 8 generated a duration of 1 point, 10 to 16 a duration of 2 points, 18 to 24 a duration of 3 points, and so on, up to a duration of 8 points. The means of deriving the duration of sounds was more involved. According to document JC/24, durations of sounds were “given by [the hexagram] number in relation to that [type’s] distribution.” Within the span of the distribution table for each event type, lower hexagram numbers would generate short durations, and higher numbers would generate longer durations. The precise duration was calculated by subtracting the lowest number in the event’s span in the table from the hexagram number and adding one. Hence, if the event table contains a span of 19 to 34 for line events, a hexagram number of 19 would represent a line of 1 point duration, while 21 would represent a line of 3 points duration, and so on up to 33, which would represent a line of 15 points duration. Hence, the size of the span for an event in the table determined not only its probability in the phrase, but its maximum possible duration as well.
Cage tossed hexagrams, determined one sound or silence at a time, until all the points in a given phrase were used. If the last sound or silence ran over into the next phrase, the appropriate number of points was deducted from the start of the next phrase. The records of these operationsare incomplete. JC/25 contains the events for the second phrase of the second string piece (1′ 5 1/2” for a String Player), and JC/26-27 list the events for the first two phrases of the third piece (1′ 1/2” for a String Player).[9] Figure 6-5 is a summary of the contents of JC/25. At the top is the distribution table for the event types in this phrase, based on the numbers 5, 11, 34, 36, 43, and 61. Under that is the list of events, with the hexagrams number thrown, sound type (or silence), and the duration.[10] The other two event-list worksheets contain similar notations.

After the basic information about the sounds and silences had been obtained, Cage determined more specific characteristics of each sound event. The types of determinations made depended on the particular event type involved. There were to be four different ways to play point events, for example:[11] ordinario (notated in the score by simple points), stopped against the fingerboard (notated with a dagger, stopped against the fingernail (notated with an x, and points played with a slide following the pluck. This last category of points had four further sub-categories: downward slides (down arrow, upward slides (up arrow), down-up slides (U), and up-down slides (inverted U).
In the case of line events, there were two further decisions to be made. Line events could be constant or intermittent in time (as described earlier), and could be played either ordinario or as harmonics. For aggregate events, there were six categories: double, triple, or quadruple stops played either constantly or intermittently in time. If a triple or quadruple stop was obtained, the direction of its breaking was also randomly chosen. Angle and curve events could be either constant or intermittent in time. Noise events of either the point or line type had no further characteristics to be determined. A summary of the seven event types and their secondary characteristics is found in JC/23 (Figure 6-6a), and is summarized in Figure 6-6b.
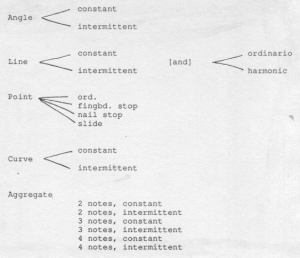
Referring again to Figure 6-5, we can see examples of how secondary characteristics were obtained. The distribution tables for each relevant secondary characteristic are on the right-hand part of the figure. To the right of each sound event in the list (at the left of the figure) are its secondary characteristics.[12]
Once the events of the piece had been determined and listed on the worksheets, Cage would turn to the actual drawing of the events in the score.[13] First, Cage would measure off the phrase lengths on paper, and inscribe the proper number of points, the location of points determined by observing imperfections in the paper. This done, he began drawing the sound events, coordinating the abstract characteristics of the sound event with the precise pitch and time information given by the points. Durations of all events and silences were measured by counting the points from left to right. Lacking the original graphic score, we cannot say precisely how the points were used in determining the pitch shape of sound events. Presumably the first point of each event would determine its starting pitch. For point and line events, this was the only pitch involved, but in aggregate, angle, or curve events, other intermediate points of the event’s duration must have been used to determine the other pitches of aggregates, and the pitch contours of the angles and curves.
Once this much of the score was drawn, Cage worked on the bowing for the piece. We do not have any documents relating to the determination of bowing pressure for these pieces. What seems likely is that Cage inscribed an arbitrary number of points on the graph score in the band reserved for bowing pressure, and used the vertical placement of these points to obtain the pressure contours for each event. The precise horizontal placement of the points was irrelevant, since the beginnings and endings of pressure notations had to be strictly coordinated with the sound events already determined.
The three remaining bowing notations (up and down bows, bowing material, and location) were determined using I Ching tables. There were three possibilities for up and down bow notations (up, down, or no notation), two for bowing material (hair or wood), and seven for bowing location (B, BN, NB, N, NF, FN, or F). Random distribution tables were obtained for each of these three notations for each phrase. Examples of these are found in JC/25 (see Figure 6-5b, bottom).
The general outline of this system was maintained for the rest of “The Ten Thousand Things”. Phrase tempi and densities were determined, followed by the general event characteristics and durations. These, together with the randomly-drawn points, were then used to draw the score. Any other notations (such as amplitudes) would then be taken care of, and the score copied.
Unfinished Piece for Magnetic Tape (1953?)
In outlining his conception of “The Ten Thousand Things” for Boulez in May of 1953, the only piece Cage specifically referred to was one for tape. Although no such tape piece survives, it would seem that Cage’s plan for “The Ten Thousand Things” included a work for tape, and (considering the early date of the letter to Boulez), that such a tape piece may have been the first in the new project to have been conceived. Notes, worksheets, and a partial score exist for a tape piece that follows the structure and general method of composition for “The Ten Thousand Things”.
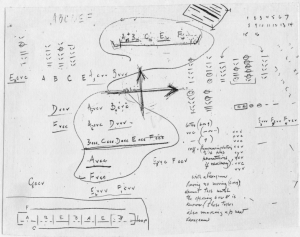

The first of these documents is JC/130 (Figure 6-7a), a page of notes, an excerpt of which is transcribed in Figure 6-7b. In these notes, Cage was clearly searching for a new way of selecting sounds for a tape piece, using the sounds of Williams Mix as a model. The page consists largely of coded descriptions of sounds similar to those used in Williams Mix (e.g., Avcv, Fvcc, etc.) and a few rather cryptic notes, such as those transcribed in Figure 6-7b. It appears that Cage’s intention at the time was to obtain as many aspects of a sound as possible from a single hexagram. The type of sound (its “letter” A-F) would be determined by the location of any “moving” lines (those assigned number values of 6 or 9). If there were more than one moving line, then a multiple-source sound was indicated. The variability or control of the sound’s parameters (the pattern of v’s and c’s) would be given by the patterns of strong and weak lines in the hexagram. If the hexagram contained a moving strong line (i.e., a line with number value of 9), then that sound was to employ a tape loop (notated, as in Williams Mix, by underlining the sound descriptor). Finally, the “n” factor used to convert rhythmic structure into tape lengths in Williams Mix is referred to here as a “coefficient”, and is arrived at by relating the hexagram’s number to 16 (e.g., hexagrams 1 to 4 give a coefficient of 1, 5 to 8 a coefficient of 2, etc.).
The particular method outlined on this page was never actually used in a composition, but would seem to be related to Cage’s desire, following Williams Mix, to write a piece for tape which would “involve computation rather than the [charts and] cards with their character of uniqueness.”[14] The method described in JC/130 would seem to be an attempt to derive sounds by such computation via the hexagrams. The basis for the “Ten Thousand Things” system was also direct computation of sounds by means of hexagrams, although in a different way. Perhaps this page of notes represents Cage’s first attempts at developing such a system for use in a tape piece — it could very well be what he was working on when he wrote his letter to Boulez on May 1st, where he complained that “what is clear [in my ideas] is made more or less pointless by rather crucial obscurities.”[15]

Like JC/130, Documents JC/131 and DT/15-22 all relate to a tape piece with Williams Mixsounds, but this time with a method closer to that of the six short string pieces of 1953. JC/131(transcribed in Figure 6-8). gives a list of the sound characteristics to be determined and the overall structure of the piece, which is the 13-part “Ten Thousand Things” structure. DT/15 is a worksheet for the piece, which follows the list of decisions given in JC/131. This document will be fully described later. Documents DT/16-22 are a partial score for the piece, with DT/16 being a title page (with the title “The Ten Thousand”), and the remaining six pages being the score for the first section of the piece. DT/15 is connected with the pages of the score in that they are all on the same type of paper, and in that the sound descriptions found on DT/15 match those in the score.
None of the documents bears a date, so it is not clear when the partial score was made. Since Cage was clearly thinking of a tape piece early on in his work on “The Ten Thousand Things”, and since the sounds are exactly like those of Williams Mix (and would thus have had to draw on the resources of “Project: Sound”), it would seem likely that this piece was written sometime in 1953, soon after the May 1st letter to Boulez describing his new ideas. There are periods of two weeks between the first and second, and between the second and third of the six string pieces — perhaps Cage was working on the tape piece during these intervals, or perhaps he worked on it after finishing the sixth string piece in July of 1953.
The score for the tape piece (documents DT/17-22) is similar to that of Williams Mix: it is a full-scale drawing of the tape itself, showing the pattern of splicing. The score is drawn on six sheets of blue quadrille graph paper, 17 by 22 inches in size. A “system” on these sheets is one inch wide and extends 15 inches across, so that one system equals one second of tape (given a tape speed of 15 ips). There are 21 systems per page, and both sides of the first five sheets are used, so that the 11 pages represent 231 seconds of music, or 3 minutes, 51 seconds.
The sounds are drawn in the score exactly as in the score for Williams Mix: the actual spliced sections of tape are drawn and their contents given by a letter designation (e.g., Avcv). In the upper left corner of the first page there is the word “track” followed by a number that is unclear due to erasures (it may be “1” or “8”). This suggests that this tape piece was to be a multi-track piece like Williams Mix. Document JC/131 notes that there would be eight speakers, suggesting a piece with eight single-track tapes played on eight machines, much like Williams Mix. DocumentDT/15 shows a table used to select numbers from one to eight, which might represent densities of tracks, but this document also has a table used to determine “1 or 2 speakers”. Since the work on the piece never proceeded far enough to clarify such matters, we cannot tell exactly what the relationship was of this partial score to the entire work. While it may have been a single track in a multi-track work, following the design of Williams Mix, the table for “1 or 2 speakers” would suggest a single stereo tape, and not eight separate tapes. Perhaps Cage’s plan was to create eight tracks but then to mix them down to two, with the disposition of each sound with regards to the two mixed tracks determined randomly via the table. The use of a single stereo tape would certainly have been more practical than the eight-tape arrangement of Williams Mix.
The method of composition in the tape piece was essentially the same as that of the six string pieces, with the necessary variations made to accommodate the medium. First, Cage determined the tempo of each phrase. Since the piece was for tape, however, the beat structure had to be converted to clock time, so that the tape could be measured properly. To do this, Cage calculated the average tempo of each phrase by adding the starting and ending tempi and dividing by two. The number of beats in a phrase divided by this average tempo resulted in the length of the phrase in minutes. This duration multiplied by 60 gave the duration in seconds, and that duration multiplied by 15 gave the length of the phrase in inches of tape. It is likely that Cage would also determine the density of points within each phrase at this time, although no documentation exists to show how this was done.

The determination of sound events in the tape piece can be reconstructed, at least in part, by an examination of the surviving worksheet (DT/15). This worksheet contains a number of randomly-derived I Ching tables, used in the selection of the various sounds. One set of these tables is shown in Figure 6-9. While individual sound descriptions are found on this same worksheet, there is no list of the hexagram numbers thrown to generate these sounds, as exists for the string pieces. Hence, the precise details of the system are not known. It would seem likely, though, that, as in the string pieces, Cage threw a single hexagram number to determine whether the event was a sound or a silence, and to determine the duration (in points) of that event. If a sound, the same hexagram would be used to determine if the sound was a single or double source, following the divisions of sounds into single and double found in Williams Mix. For each actual source, a sound description would be built from three tables. First, there were six categories of sounds, notated as capital letters A through F, which presumably were the same six sound categories used inWilliams Mix. Next, one of the eight possible patterns of variable and controlled sound parameters (amplitude, overtone structure, and frequency) was obtained, notated as a triplet of v’s and c’s (e.g., vvc). Finally, a table was used to determine if the source was to be looped or not, a looped source being notated by underlining the sound description. If the sound was a double source, the means by which the two sources were to be combined was determined by another table. The sounds could be either mixed, notated by writing the sound descriptions next to each other (e.g., AcvvEvvc), or they could be spliced together, notated by a plus sign between the sound descriptions (e.g., Accc+Eccc). As mentioned above, the table for “1 or 2 speakers” is of unknown use, but perhaps could refer to the mix-down of the tracks: a sound could either be mixed wholly in channel 1, wholly in channel 2, or equally mixed in both.
Following this determination of sound events, the score itself was drawn. Presumably durations were measured in points as in the six string pieces. The angles of the splices were perhaps determined in a manner akin to the way angle events in the string pieces were obtained: the pattern of points could have been used to suggest the contours of the splices.
Unfinished Piece for Voice (1953?)
In addition to the unfinished piece for tape, there exists a fragment of a work for voice that uses the structure and method of “The Ten Thousand Things”. All that remains of this work is one pageof a score (document JC/132). This is a graphic score very similar in layout to the string pieces (see Figure 6-10). Time is measured horizontally in beats (2 centimeters per beat), with tempo marks at the beginning of each phrase, just as in the string pieces. The first phrase in the fragment is 24 centimeters long, or 12 beats, and thus corresponds to the rhythmic structure of “The Ten Thousand Things”. Vertically, there is a large band for pitches, in which there are point, line, angle, and curve events, and beneath this band is a band for noises with point and line events. Above both is a band for amplitudes, similar to the bowing pressure notation of the string pieces. In addition to these, between the amplitude and pitch bands, there are notations “IN” and “EX”, which apparently are breathing notations (“inhale” and “exhale”). Below these is the “text” of the piece, notated phonetically.
As there are no further documents for this piece, it is not clear precisely what method was used to produce it. The similarity of the score and the events contained within it to those of the string pieces suggests strongly that a similar method was used. In fact, the exact method of the string pieces could have been used, save that aggregate events and harmonics would not be used, bowing locations and materials would not be needed, and text would have to be added.
In fact, this one-page fragment may not even represent a plan for a piece so much as an experiment with applying the string piece method to vocal music. This theory is supported by pencilled notes on the page. These notes show Cage still making decisions as to how to design the compositional system. In particular, they deal with the relation of noise events to text and amplitude. For example, in one note, Cage decides to “give v[owels] and c[onsonants] for noises”; this text would then be “guttural or intake” sounds. Elsewhere he notes that “in breath = noise area”, and that “amp[litude] unnec[essary] for intake sounds.” Such notes show that Cage had not settled on a method for this piece, but rather was still exploring the possibilities inherent in the method derived for the string pieces.
While there is no date on this page, the use of tempi and beats suggests that it was composed before 1954, at which point Cage began notating time exclusively in minutes and seconds. The closeness of the system in this piece to that of the string pieces suggests a closeness in time — perhaps this sketch was made in the summer of 1953 while Cage was still working on the string pieces.
34′ 46.776” for a pianist and 31′ 57.9864” for a pianist (1954)
Cage and David Tudor were invited to perform at the Donaueschinger Musiktage in the fall of 1954, and for this occasion, Cage was commissioned to compose a new work for two pianos.[16] Cage used this opportunity to compose two more parts for his ongoing “Ten Thousand Things” project. The resulting work was not just a piece for two pianos, but rather consisted of two pieces that could be performed either separately or together, or with the short string pieces he had already composed. Following the practice started with those string pieces, the titles of the new works were based on their durations. 34′ 46.776” for a pianist, written for David Tudor, was the more difficult work, while 31′ 57.9864” for a pianist, written for Cage himself to perform, was “relatively easy to play.”[17] The first performance of the work was in Donaueschingen on October 17th, 1954.[18]
The new pieces were for prepared pianos, the last large works Cage would compose for that instrument. Unlike his previous works for prepared piano, Cage did not fully describe the preparations to be used for these pieces, but rather gave only general types of objects to use. The preparation tables found in the scores of the two pieces (see Figure 6-11) list the notes to be prepared and a list of the object types to be used, notated with the letters M (representing metal objects), W (representing wooden objects), C (representing cloth, fibre or rubber objects), P (representing plastic, glass, or bone objects), and X (representing objects of any type). The exact choice of objects used and their placement on the strings was left to the performer, so that the sounds of the instruments would vary from performance to performance.

In addition to the indeterminate element in preparing the pianos, Cage introduced the device of having the preparations change during the course of the work. At points throughout the score are notations “MOVE”, “ADD”, “PS”, and “CS” associated with particular pitches, and followed by a number (see Figure 6-11 for an example). These notations signified that the preparation of that pitch should be moved along the string (“MOVE”), have objects added to it (“ADD”), have one or more objects removed from it (“PS”, or “partial subtraction”), or have all preparations removed from it (“CS”, or “complete subtraction”). In the case of “ADD” notations, the type of object or objects to add is also given. The number given after each instruction represents the time (in seconds) before the next occurrence of that pitch, thus giving the performer an idea of how much time he has to effect the preparation change.

The pitch notation of 34′ 46.776” for a pianist and 31′ 57.9864” for a pianist is more or less a traditional one (see Figure 6-12). Notes are presented on the normal five-line staves with the normal treble and bass clefs. The notations [graphic] and [graphic] indicate the directions (down or up) of rolled chords. Besides simple single notes and chords, there are also clusters (notated as vertical bands) and tremolos (notated in the usual fashion). The notations “K” and “H” indicate whether the notes are to be played on the keyboard or strings (“harp”) or the piano, respectively. Notes played on the strings could be played in any of a variety of ways, the choice left to the performer: “finger-muted; pizz.; muted and pizz; struck with mallet, beater, fingers, etc.; strike or otherwise activate preparation (if any), etc.”[19] Notes played on the keys (which include all notes not explicitly given an “H” or “K” notation) could be played normally, or while touching the strings “so as to produce harmonics.”[20] All pedalling was left free.
Noises are notated between the two staves, and are of three general types: noises made on the interior of the piano, noises made on the exterior or “outside” of the piano, and noises made by “accessories”, such as “whistles, vocal noises, percussion instruments, etc.”[21] Only the general type of noise is given, notated by the letters I (inside), O (outside), and A (accessories).
The notation of time in these pieces uses clock time rather than beats. The method of converting the metric basis of the rhythmic structure to minutes and seconds was that used in the unfinished tape piece. That Cage used clock-time notation here rather than the “musical-time” notation of beats is probably due to the influence of David Tudor, who had solved the rhythmic difficulties ofMusic of changes by calculating the duration of each phrase in seconds and then using a stopwatch in performance.[22] The scale of time measurement is variable, the length in space of one second being dependent on the density of notes at that time — the shortest lengths used in the least dense passages and the longest lengths used in the most dense passages. In the score, the elapsed duration in seconds is given at regular intervals (usually — but not always — every other second), along with a “ruler” to show the current scale of time measurement. Extended silences (such as the passage from 16 to 55 seconds in Figure 6-12) are not fully written out, but are represented by short blank spaces.
There are three basic rhythmic notations used in these works. Notes with stems (but not attached to beams) are to be played as short as possible (i.e., they are points, or events of no duration). Notes of a very short duration are given by note-heads with two dots above them, the duration being the distance between these dots. Finally, notes of longer durations are given by extending the note horizontally, with the length of this horizontal line representing the duration of the note. This last notation is essentially that used by Earle Brown in parts of his Folio (1952) and 25 Pagesfor piano (1953). Notes connected by stems to a beam are “an aggregate in time” which “may be freely interpreted; by no means is a simple legato always to be inferred.”[23] As will be noted later, these beamed “aggregates in time” may be more structural than rhythmic in nature.
Finally, there are three bands of notations above the pitches, which are similar to the bowing pressure notations of the string pieces or the amplitude notations of the unfinished vocal piece. These three bands, taken together, describe the attack used by the pianist. Points in the top band represent the “degree of force” of attack for each note, with the bottom of the band being the least force. Points in the middle band represent the “vertical distance” of attack for each note, with the bottom of the band being the closest distance. Finally, points in the bottom band represent the speed of attack for each note, with the bottom the band being the fastest attack. Each point drawn within these bands corresponds to one note in the score below it. In the case of some aggregates, multiple notations are given, these being differentiated by one, two, or three angled lines drawn from the points. Perhaps because of the extreme difficulty of performing from such a detailed notation, Cage has added the following “escape hatch” to the score: “the notation may be read in any `focus’ (as many or as few of its aspects as desired being acted upon).”[24]
Both 34′ 46.776” for a pianist and 31′ 57.9864” for a pianist follow the two-level rhythmic structure of “The Ten Thousand Things”. At the phrase level, they are formed of groups of five phrases with lengths of 12, 16, 28, 26, and 18 beats each, respectively (although the conversion to clock time has removed any traces of this beat structure). At the large scale, the pieces consist of 28 of these phrase group units divided into five sections of 3, 7, 2, 5, and 11 groups each, respectively. As can be seen, these are the first five section lengths of the 13-section large scale structure of 100 groups Cage had decided upon for “The Ten Thousand Things”. The decision to compose only the first five sections was perhaps made due to time restrictions (since Cage was working on a deadline), or perhaps the idea was to produce a work lasting roughly a half an hour, and the 28-unit structure was a convenient frame for this. In any event, the 28 units are marked by dotted lines in the score (e.g., at 57.3762” in Figure 6-12), and Cage indicates that any number of these units may be performed in any combinations.[25] Section boundaries are also noted in the score in the same way.
Unfortunately, the documentation for the composition of these works is incomplete. The bulk of the material that survives consists of six large rolls of graph paper. Three of these (DT/24-26) are parts of the original graphic score for 34′ 46.776” for a pianist. According to these rolls, the score originally consisted of six rolls — only rolls two, four, and six survive. The other three rolls of graph paper (DT/28-30) are the complete graphic score for 31′ 57.9864” for a pianist. There are two other single sheets of graph paper (DT/23 and DT/27) whose significance is unclear.
The graphic scores consist of points (presumably the points determined by paper imperfections) within a vertical space that represents the 88 keys of the piano, plus the three types of noises. There are also areas for the three attack notations (force, distance, and speed). Time is measured horizontally: in the case of the score for 34′ 46.776” for a pianist, 2 inches of graph equals one second, while in the score for 31′ 57.9864” for a pianist, 1 inch of graph equals one second. Some of the points (but not all) have been darkened to indicate the notes of the pieces. Also present in this score are the beamed “aggregates in time” and the horizontally-extended notes, while the stemmed notes of no duration appear in the graphic score as simple points. The graphic scores also contain the notations for changing preparations (“ADD”, etc.).
What is lacking in documentation for the piano pieces is the sort of event descriptions found for the six short string pieces or the tape piece. Such lists of events allow us to isolate individual musical features of the score and to evaluate the importance of Cage’s choices as to event types. Lacking such documentation of the types of events Cage used in these works, we have no basis for deciding which points — or even how many points — combine in any place to form a single, compositionally coherent structure.
Some information can be gleaned from Cage’s lecture “45′ for a Speaker”, written in 1954 as an accompaniment to “The Ten Thousand Things”. This lecture consists of a collage of old and new texts, and among the fragments are clear references to the composition of 34′ 46.776” for a pianistand 31′ 57.9864” for a pianist. At one point Cage explains:
To determine the number of imperfections in a given space, coins are tossed. That number of spots is then potentially active. Subsequent tosses determine which are actually active. Tables are arranged referring to tempi, the number of superimpositions, that is to say number of things that can go on at once, sounds & silences, durations, loudnesses, accents. Sounds together (suffice it to say). Structure is of no importance, however, I go on having it by chance to determine first the relative probability of the three, and then to determine which of the three happens.[26]
The method described here of inscribing points and then determining which of those points are “actually active”, suggests the method that was clearly used in composing 27′ 10.554” for a percussionist, which will be described later. In brief, that method, and the method implied in Cage’s comments here, selected groups of points as “active” and then applied event structures (selected by means of the I Ching) to these points. Such a method, in which a collection of points have a structure adapted to them, is the opposite of that used in 26′ 1.1499” for a string player, where the structures were selected first and the points applied later. Later in “45′ for a Speaker”, Cage gives more reason to believe some variant of this method was used, and offers clue as to the event structures used:
Given a number of actually active points, they are an aggregate, a constellation, they can move about among themselves and it becomes necessary to classify the kinds of aggregates, say constant and again intermittent.[27]
In 27′ 10.554” for a percussionist, the points could be used to form point events, line events, or a mixture of point and line events. Cage’s comments about aggregates, constellations, and “aggregates in time”, along with observation of the score, suggests that he may have used a similar division in the piano pieces. Here the active points may have been grouped into single notes, aggregates, or constellations (“mixes” or “aggregates in time”) of single notes and aggregates. These last-named events would be represented in the score by the beamed groupings of events. Without further documentation, we cannot know for certain how the points of the graphic score were shaped into events.
A point of interest in these excerpts from “45′ for a Speaker” is Cage’s reference to a table for “number of superpositions.” This suggests that in the piano pieces, unlike the string pieces, Cage had revived his ideas of layered vertical structure or “superimposed parts”, used in the chart works of 1951-1952. Such a layered structure would not have been appropriate for a solo string piece, since the simultaneities involved would have been impossible to play. However, a multi-layered texture for a piano work was quite reasonable. In the graphic scores for these two pieces, there are notations at the beginning of each phrase that may relate to such a vertical structure In31′ 57.9864” for a pianist, at the start of each phrase appear the letters A to D, each followed by a pair of numbers (e.g, “51/61”). In 34′ 46.776” for a pianist, similar notations occur, but with only the letters A and B. The letters may each refer to one superimposed part, and the pair of numbers following the letters (which are all in the range 1 to 64, except for the various occurrences of “0/0”) may refer to a partitioning of the I Ching for that superimposed part in that phrase. If these two numbers do represent an I Ching partition, then this triple-division would be further reason to believe in a division of events into single, aggregate, and constellation types. The periodic occurrences of “0/0” would then represent an inactive layer. In any case, the use of four layers in 34′ 46.776” for a pianist and only two layers in 31′ 57.9864” for a pianist, along with the different scales of time measurement in the two graphic scores, would make the former work (the one intended for David Tudor) more virtuosic and more demanding of the performer than the latter.
26′ 1.1499” for a string player (1955)
After returning from his 1954 European tour, Cage decided to add to the six short string pieces and compose a piece for string player that was equal in size to the two piano pieces he had just finished. The large string piece, then, would consist of 28 units forming the 5 sections in proportions {3, 7, 2, 5, 11}. It will be recalled that the six short string pieces Cage had composed in 1953 were each one unit long. Thus they could be directly incorporated into the new large piece, saving Cage some time in composition. As it turned out, Cage decided to use only the first five of the short string pieces; these were used to form the fourth section of the new large work. The remaining four sections, totalling 23 units, were newly composed by Cage with assistance from David Tudor. The resulting piece was titled 26′ 1.1499” for a string player, and was premiered on October 15th, 1955, with Harold Coletta performing on viola, at which time it was played along with 31′ 57.9864” for a pianist and 34′ 46.776” for a pianist.[28]
The large string piece is notated in the same fashion as the short string pieces, with one slight exception. Cage decided to follow the practice of 31′ 57.9864” for a pianist and 34′ 46.776” for a pianist and notate the new work in clock time in lieu of beats. The 23 newly-composed units were directly composed in clock time, but the 5 older pieces remained notated in beats. To adapt these older pieces, Cage calculated the durations of their phrases in seconds and added markings giving these elapsed durations to the scores of the older pieces. Otherwise the older pieces were left unaltered.
The method of composing 26′ 1.1499” for a string player was virtually identical to that used for the six short string pieces. This is confirmed by the extant documents for this piece. JC/28-33are worksheets detailing the determinations of tempi and densities for each phrase of the new units. The lists of events for the new units are found in documents JC/34-105, with JC/90-105(the event lists for the last section) being written in David Tudor’s hand. Both of these sets of worksheets contain the sorts of notations found in the corresponding worksheets for the six short string pieces.
Documents JC/106-124 give the determinations of bowings for the new music. These include the notations found in the earlier pieces (up and down bows, and notations for using hair or wood), along with a new determination. This new aspect of the bowing is expressed by the letters S, A, and C — there is no explanation on the worksheets for these letters. Upon matching these letters with the appropriate events in the score, however, their meaning becomes apparent. In the short string pieces, the bowing pressure for an event of notated duration (i.e., all events other than points) was indicated as a curve. In the new piece, Cage decided to have the bowing pressure contours parallel the different types of pitch contours: they could either be horizontal lines, lines at some angle, or curves. The letters S, A, and C, then, stand for “Straight”, “Angle”, and “Curve”, and denote the type of pressure contour used for each event.
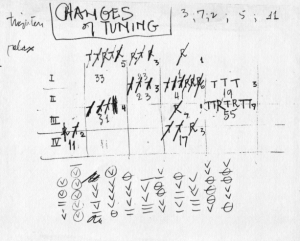
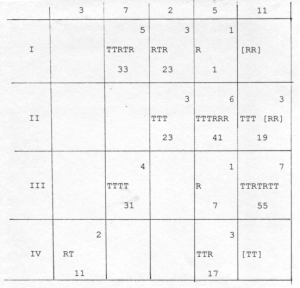
The other addition to the system of composition regarded the tuning of the instrument. Perhaps to parallel the changes of preparations in the piano pieces, Cage decided in the new string piece to have the tuning of the instrument change during the piece. This is represented in the score by periodic notations “increase” and “decrease”, referring to the tension of a particular string. Document JC/125 (Figure 6-13a) is a worksheet involved in the determination of these tuning changes, and is summarized in Figure 6-13b. The roman numerals down the left side refer to the four strings of the instrument, and the five columns of notations correspond to the five sections of the piece. I Ching hexagram numbers were tossed for each of the twenty cells in this chart. Even numbers indicated that no change in tuning was to occur for that string in that section of the piece. Odd numbers caused tuning changes — hexagram numbers 1-7 caused one tuning change in the section, numbers 9-15 caused two tuning changes, and so on up to eight tuning changes for one string in one section. In the chart, the hexagram numbers appear at the bottom center of the cells (the even hexagram numbers do not appear in the chart), while the corresponding numbers of tuning changes appear in the upper right corner of the cells. Cage would then determine in some way the actual changes to be made, notated in the chart by the letters “R” (for “relax”) and “T” (for “tighten”). How he determined the specific locations in the score at which these changes were to be made is not known. Also, it should be noted that the notations on JC/125 do not correspond exactly with what appears in the score. In particular, there are six tuning changes in the last section that do not appear in the chart (these are given in brackets in Figure 6-13b).
27′ 10.554” for a percussionist (1956)
After finishing the extension of the string piece, Cage composed one final score in “The Ten Thousand Things”. This work, for percussion, was to follow the same 28 unit, 5 section structure of the two piano pieces and the string piece, and was similarly given its title from its duration: 27′ 10.554” for a percussionist. Although completed in January of 1956, it was not performed until February of 1962, when it was given a performance by Siegfried Rockstroh with Mauricio Kagel in Munich.[29]

27′ 10.554” for a percussionist is notated in clock time (see Figure 6-14), although here the scale of notation (one inch equals one second) is constant throughout the score, whereas in the string and piano pieces the scale varies according to the density of events. The use of a constant scale is the result of Cage abandoning the intermediate stage of a graphic score, used in previous pieces; here the notes were directly drawn onto the fair copy. There are four systems, 15 inches long, on each page, so that one page of the score corresponds to one minute’s duration. As in Music for piano 53-68, the systems are not drawn where there are extended silences, so that large portions of some pages are blank.
Vertically, each system consists of four bands. The four lines marked “M”, “W”, “S”, and “A” represent the centers of these bands: their boundaries are not shown in the score. The letters refer to the types of instruments to be used. “M” stands for “metal”, “W” for “wood”, “S” for “skin”, and “A” for “all others, e.g., electronic devices, mechanical arrangements, radios, whistles, etc.”[30] The notes of the piece are to be played by any instruments, so long as they conform to the general type within whose band a particular note falls. Cage clearly intended a diverse assortment of instruments and playing techniques:
A virtuoso performance will include a wide variety of instruments, beaters, sliding tones, and an exhaustive rather than conventional use of the instruments employed. For example: a gong may be suspended or placed on a mat, struck with metal, felt, yarn, wood, rubber, etc.[,] beaters at points on the edge or center or anywhere between. It may be lowered into and/or raised out of a tub of water. A tremolo between suspended gongs facing one another is another use. And directional changes following the attack are also effective.[31]
Whereas in the string and voice pieces (and the graphic score of the piano pieces) Cage had used the vertical dimension of the score to notate pitch, in this work pitch notation was unnecessary, and hence Cage used the vertical dimension to notate amplitude. The four lines, representing the centers of the four bands of sounds, signify a dynamic of mf, so that notes above these lines are louder sounds, while those below are softer sounds. The notes themselves (see Figure 6-14) are mostly points, but also include some line segments (although none appear in the figure), which thus represent notes of some duration (presumably tremolos) with a particular contour of changing dynamic. In the case of metal instruments, some notes have “hooks” on them, which indicate “laissez vibrer“.[32] If notes occur close to the boundary between two sound categories, a vertical line, attached at one end to the note and at the other to one of the center lines, is drawn to identify unambiguously which category is involved. These vertical lines are thus not compositionally significant, but are simply a notational convenience. All that is notated for a given sound, therefore, is the general type of instrument to be used, the point of attack, and the relative dynamic. In the case of line events, the duration is also given, along with the changing dynamic. Cage indicates in the score that the piece “may be performed as a recording or with the aid of a recording.”[33] This latter was apparently done at the premiere, since Kagel is listed as performing on “magnetic tape.”[34]
The structure of 27′ 10.554” for a percussionist is identical to that of the piano and string pieces: 28 units, each divided into 5 phrases, and subsequently grouped into 5 sections with proportions {3, 7, 2, 5, 11}. As in the other pieces, any number of these units can be performed in any horizontal or vertical combination. In the performance note for this piece, however, Cage adds the proviso that “a performance with string player and/or pianists may be made providing the latter use an equal number of structural units of their parts.”[35] Although the earlier pieces did not explicitly mention that each performer in an ensemble realization of the work should play the same amount of music (measured in structural units), such a conception is implied by Cage’s having composed identical amounts of music for each piece (28 units). Also, in an unpublished performance note for 26′ 1.1499” for a string player (document JC/129), Cage presents the possibility of a performance of that work by a string quartet, with each player using seven units of the score.
The first step in the process of composing 27′ 10.554” for a percussionist was the same as for the string and piano pieces: the determination of tempi and densities for each phrase of the rhythmic structure. The tempi were then used to calculate the duration in seconds of each phrase. Documentation for this process is found in JC/133 (lists of tempi, average tempi, and durations in seconds) and JC/134-136 (calculations of densities). The determination of individual events was somewhat different from the method used in 26′ 1.1499” for a string player. Documents JC/137-158 are worksheets recording this process. Although these worksheets do not list the hexagram numbers used, they do contain actual drawings of the hexagrams, which allows us not only to identify the hexagram numbers, but also to establish the precise order of determinations Cage made, by relating the order of the hexagrams on the page to their use in determining sound events.
First, Cage obtained numbers which determined both sound and silence, and the duration of that sound or silence. Even numbers signified silences, odd numbers signified sounds, as in the string piece. Durations were more simply calculated than in that earlier work, however. Here, the sound-silence hexagram number was itself the duration, in terms of points. Hence, the range of possible durations for all sounds and all silences was the same at all times: 1 to 64 points. Sound-silence hexagrams were obtained for each sound in the phrase, until the total number of points was used up. If the last event ran over the phrase’s end, the appropriate number of points was deducted from the beginning of the next phrase. Once all the sounds and silences were determined, Cage obtained hexagram numbers for each sound event in the phrase to determine the number of “active” or sounding points within the number allotted it. In other words, although a sound event may have had a duration of twenty points, not all of these points may have actually been sounding. The duration, therefore, was not strictly the duration of an event, but delimited the space within the phrase that a sound event occupied. The number of active points would then determine how much of the whole duration (or “potentially active” points)[36] consisted of actual sound. The newly-obtained hexagram number, if less than or equal to the total duration, would represent the number of active points within that duration. If the active-points hexagram was greater than the duration, Cage divided it by the total duration, and the remainder of this division would be the number of active points for that event.
Once the number of active points within each sound duration were obtained, Cage determined the event types. There were only three types of events: points, lines, and mixtures of points and lines. An I Ching table for these three types was created by tossing two hexagrams to be used as the dividing points. Then hexagrams were obtained for each sound to determine the event type of that sound, based on the table.

Figure 6-15 shows an example of this process, based on the worksheet for the second phrase of the thirteenth unit of the piece (document JC/144, Figure 6-15a), which corresponds to music running from 800.120 seconds to 821.936 seconds in the score. The numbers in the leftmost column are the sound-silence hexagrams. As can be seen, even numbers correspond to silences, odd numbers to sounds. These numbers also represent the total duration of each event. This particular phrase has a total length of 274 points, and has thirty points deducted to complete the last sound of the previous phrase. Summing the durations of the events in the phrase, and adding the thirty “overlap points”, we get a total of 279 points, so that 5 points are deducted from the next phrase.
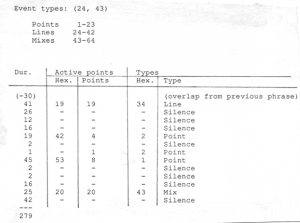
The next two columns give the hexagram numbers thrown to determine the numbers of active points in sound events, and then the resulting number of active points. In the case of the first sound, the hexagram number 19 is smaller than by the duration 41, so a total of 19 points in the duration are active. In the next sound, the division of active-points hexagram number (42) by the duration (19) leaves a remainder of 4, which thus becomes the number of active points. No hexagram number was thrown for the next sound, since the total duration was only one point. The calculations of active points in the remaining sounds are similar.
The numbers obtained to create the table of event types are shown at the top of the figure, along with the derived table: numbers from 1 to 23 produce point events, 24 to 42 produce lines, and 43 to 64 produce mixtures. The last two columns of the figure show the hexagrams numbers used to determine the type of each sound event, and the actual resulting type.
Once these event lists were made, Cage inscribed the points on the score and then used the event lists to draw the notes. Counting points, he would determine the boundaries of each event based on its total duration. The actual drawing of notes was based on the number of active points within these boundaries. If the event was of the point type, then Cage would darken that many points to form a “cloud” of notes. If the event was a line event, then the active points were used to guide the contours of the line segments. Finally, if the event were a mixture, then the active points would be arranged into some combination of points and lines. It is not clear how Cage selected the active points in the total duration. Perhaps since the decision had been so restricted by previous determinations, Cage felt he could simply choose points arbitrarily, based on no particular system at all.
Notes
[1] John Cage, Letter to Pierre Boulez, May 1, 1953, JCA-16.
[2] John Cage, “45′ for a Speaker” (1954), Silence (Middletown: Wesleyan University Press, 1961), p. 182.
[3] Noting that all the structural numbers in both pieces are integers, and that they are all less than or equal to 16, it might be speculated that Cage simply used I Ching hexagram numbers related to 16 to arrive at the structural proportions of both works. The number of parts in each structure (six in Williams Mix and thirteen here) might have been derived in the same fashion.
[4] Cage, “45′ for a Speaker”, p. 82.
[5] Lao Tzu, The Way of Lao Tzu, Wing-Tsit Chan, trans. (New York: Bobbs-Merrill Co., 1963), p. 176.
[6] John Cage, “Performance note”, 26′ 1.1499” for a string player (New York: Henmar Press, 1960), page c.
[7] Ibid.
[8] It is of interest to note the change in Cage’s plan as demonstrated in JC/20. In his first attempt at partitioning the I Ching, he tried using the hexagram numbers in the order thrown, so that each subsequent number would have to be “larger than the preceding.” After trying this out (in the first I Ching table of Figure 6-?), Cage realized that it would be more efficient to use the first three numbers thrown, and then arrange them in ascending order (as in the next I Ching table of the same figure).
[9] The versi of JC/26-27 were later used as worksheets for the later, larger string piece.
[10] The durations of silences do not actually appear on the document, but are inferred from the hexagram numbers.
[11] Cage, “Performance note”, 26′ 1.1499” for a string player, page c.
[12] The hexagram numbers thrown to obtain these characteristics are not noted on the document.
[13] Mr. Cage recalls that these points were drawn on graph paper and then transcribed to the final score (Conversation with the author, 12/29/87). If so, the graph score is now lost.
[14] John Cage, Letter to Pierre Boulez, n.d. [July 1952?], JCA-11.
[15] John Cage, Letter to Pierre Boulez, May 1, 1953, JCA-16.
[16] John Cage and Robert Dunn, John Cage [catalog of works] (New York: Henmar Press, 1962), p. 26.
[17] Ibid.
[18] Ibid., p. 27.
[19] John Cage, “Performance note”, 34′ 46.776” for a pianist (New York: Henmar Press, 1960), p. ii.
[20] Ibid.
[21] Ibid.
[22] Tudor’s copy of the Music of changes score contains these time notations, and he still possesses several pages of calculations giving the duration of each measure of that work.
[23] Cage, “Performance note”, 34′ 46.776” for a pianist, p. ii.
[24] Ibid.
[25] Ibid.
[26] Cage, “45′ for a Speaker”, p. 159.
[27] Ibid., p. 163.
[28] Cage and Dunn, p. 27.
[29] Cage and Dunn, p. 27.
[30] John Cage, “Performance note”, 27′ 10.554” for a percussionist (New York: Henmar Press, 1960).
[31] Ibid.
[32] Ibid.
[33] Ibid.
[34] Cage and Dunn, p. 27.
[35] Cage, “Performance note”, 27′ 10.554” for a percussionist.
[36] Cage, “45′ for a Speaker”, p. 159.

Pingback: why i stopped to write “pieces” | ccloudblog
Pingback: John Cage - Music Banter